Figury geometryczne – jakie są? Poznaj je wszystkie!

Uaktualniene dnia 18 lipca, 2025 przez Redakcja Xportal.pl

Figury geometryczne stanowią podstawę wielu dziedzin matematyki i są istotne dla rozwijania zdolności analitycznych. Przedstawiamy kluczowe pojęcia, takie jak punkty oraz proste, a także dzielimy figury na płaskie i przestrzenne. Czytelnicy odkryją różnorodność wielokątów oraz poznają różne rodzaje trójkątów. Dodatkowo, dowiedzą się o klasyfikacji i zastosowaniach czworokątów.

Podstawowe pojęcia w geometrii

Podstawowe pojęcia geometrii odgrywają kluczową rolę w matematyce, stanowiąc bazę do rozwijania bardziej zaawansowanych teorii. W tej dziedzinie wyróżniamy kilka istotnych elementów:

• punkt,
• prosta,
• odcinek,
• półprosta,
• łamana.

Punkt to najmniejszy element bez wymiarów, który zazwyczaj oznaczamy małą literą lub kropką na rysunku. Prosta to nieskończona linia, która nie ma ani początku, ani końca, a definiują ją dwa punkty, przez które przechodzi. Odcinek jest odmienny, gdyż ma jasno określony początek i koniec. Półprosta startuje w konkretnym punkcie i rozciąga się w nieskończoność w jednym kierunku. Łamana natomiast składa się z połączonych końcami odcinków, tworząc kształt otwarty bądź zamknięty.

Zrozumienie tych fundamentalnych pojęć jest niezbędne, gdyż stanowią one podstawę do zgłębiania bardziej skomplikowanych figur geometrycznych, takich jak kwadraty, trójkąty czy koła. Te formy są kluczowe w edukacji matematycznej, wspierając rozwój umiejętności analitycznych i rozwiązywania problemów. Wiedza o figurach geometrycznych ma także praktyczne zastosowanie w projektowaniu, architekturze i inżynierii, gdzie precyzyjne obliczenia są nieodzowne. Dzięki geometrii możemy również obliczać takie właściwości jak pole powierzchni czy objętość, co jest istotne w wielu dziedzinach nauki i techniki.

Punkt – podstawowe pojęcie

Punkt w geometrii to abstrakcyjna idea pozbawiona wymiarów. Zazwyczaj przedstawia się go jako małą literę lub kropkę na diagramie. Nie posiada ani długości, ani szerokości, ani wysokości, lecz wyznacza określoną lokalizację w przestrzeni. W figurach geometrycznych punkty często stanowią wierzchołki trójkątów czy czworokątów. Pomimo swojej prostoty, punkt stanowi fundament geometrii i wspiera naukę matematyki oraz rozwijanie zdolności analitycznych.

Prosta – właściwości i oznaczenia

Prosta w geometrii to linia, która nie ma ani początku, ani końca, i jest nieskończona. Stanowi jeden z fundamentalnych elementów w tej dziedzinie matematyki. Oznacza się ją zazwyczaj małą literą, co pozwala łatwo odróżnić ją od odcinków czy półprostych. Charakterystyczną cechą prostej jest to, że przez dowolne dwa punkty można przeprowadzić tylko jedną taką linię.

Choć prosta nie ma wymiarów, takich jak długość czy szerokość, odgrywa kluczową rolę w definiowaniu innych figur geometrycznych, takich jak trójkąty czy czworokąty. Zrozumienie jej właściwości jest przydatne w matematyce, projektowaniu technicznym i innych dziedzinach wymagających precyzyjnych obliczeń i modelowania przestrzennego.

Klasyfikacja figur geometrycznych

Podział figur geometrycznych obejmuje figury płaskie oraz przestrzenne. Do pierwszej kategorii zaliczamy takie kształty jak:

• kwadrat,
• prostokąt,
• trójkąt,
• koło.

Figury te mierzą się długością i szerokością. Wyróżniają się one różnorodnymi cechami, takimi jak liczba boków czy symetria. Przykładowo, kwadrat charakteryzuje się czterema równymi bokami i kątami prostymi, a trójkąt występuje w różnych formach w zależności od długości boków i miar kątów.

Figury przestrzenne, takie jak:

• sześcian,
• kula,
• stożek,
• walec,

mają trzy wymiary: długość, szerokość oraz wysokość. Każda z tych brył posiada unikalne właściwości, na przykład objętość i pole powierzchni, które oblicza się za pomocą specjalnych wzorów matematycznych. W dziedzinach takich jak architektura i inżynieria, precyzyjne obliczenia przestrzenne są nieodzowne i mają kluczowe znaczenie.

Zrozumienie klasyfikacji figur geometrycznych jest fundamentalne w edukacji matematycznej, gdyż wspiera rozwój umiejętności analitycznych i zdolność rozwiązywania problemów. W szkole podstawowej uczniowie poznają, jak rozpoznawać różne figury i obliczać ich pola oraz objętości, co stanowi ważny element nauki matematyki.

Figury płaskie i przestrzenne – różnice

Figury płaskie i przestrzenne różnią się ilością wymiarów.

Przykłady figur płaskich to:

• kwadraty,
• prostokąty,
• koła.

Figury te charakteryzują się dwoma wymiarami: długością i szerokością i są one przedstawiane na płaszczyźnie.

Natomiast figury przestrzenne, takie jak:

• sześcian,
• prostopadłościan,
• kula,

posiadają trzy wymiary: długość, szerokość i wysokość. Dzięki temu wypełniają przestrzeń.

Bryły, czyli figury przestrzenne, cechują się również dodatkowymi właściwościami, jak objętość i pole powierzchni. Te cechy odgrywają istotną rolę w różnych dziedzinach, takich jak architektura czy inżynieria. Znajomość różnic między figurami płaskimi a przestrzennymi jest fundamentalna w matematyce, ponieważ umożliwia dokładne obliczenia geometryczne.

Podstawowe figury płaskie i ich właściwości

Podstawowe figury płaskie obejmują wielokąty, takie jak trójkąty i czworokąty, które różnią się między sobą liczbą boków oraz kątów. Są to figury geometryczne, a ich właściwości zależą od liczby boków. Trójkąt, na przykład, charakteryzuje się trzema bokami i sumą kątów wewnętrznych równą 180 stopni. Czworokąty, do których zaliczamy kwadraty i prostokąty, posiadają cztery boki, a ich kąty wewnętrzne łącznie wynoszą 360 stopni.

Każda z tych figur ma jednak swoje specyficzne cechy, co jest istotne dla zrozumienia geometrii. Trójkąty możemy wyróżnić jako:

• równoboczne,
• równoramienne,
• różnoboczne.

Różnią się one długością boków. Czworokąty, takie jak kwadrat czy trapez, różnią się szczegółami dotyczącymi boków i kątów. Kwadrat, na przykład, ma cztery równe boki i kąt prosty przy każdym wierzchołku, podczas gdy trapez charakteryzuje się jedną parą boków równoległych.

Znajomość tych właściwości jest kluczowa w edukacji matematycznej. Uczniowie uczą się klasyfikować figury, a także obliczać ich pola oraz rozwiązywać różnorodne problemy geometryczne. Matematyczne wzory stosowane do obliczania pól czy obwodów stanowią podstawę bardziej zaawansowanych zastosowań w projektowaniu i inżynierii.

Wielokąty – liczba boków i różnorodność

Wielokąty to płaskie figury, które można odróżnić na podstawie liczby ich boków. Ta cecha wpływa na ich różnorodność i sposób klasyfikacji w geometrii. Na przykład, trójkąty posiadają trzy boki, a suma ich kątów wewnętrznych wynosi 180 stopni. Z kolei czworokąty, takie jak kwadraty czy prostokąty, mają cztery boki i łączna wartość ich kątów to 360 stopni.

W zależności od długości boków i kątów, wielokąty można podzielić na różne kategorie. Ta wiedza jest kluczowa w edukacji matematycznej oraz rozwijaniu zdolności analitycznych. Dzięki niej uczniowie potrafią:

• klasyfikować figury geometryczne,
• obliczać ich pola,
• obliczać ich obwody.

Zrozumienie różnorodności wielokątów odgrywa również istotną rolę w nauczaniu podstaw geometrii na poziomie szkoły podstawowej.

Trójkąty – rodzaje i charakterystyka

Trójkąty to fundamentalne figury geometryczne, charakteryzujące się trzema bokami oraz trzema kątami. Możemy je podzielić na podstawie długości boków oraz miar kątów.

Wyróżniamy trzy główne rodzaje trójkątów:

• trójkąt równoboczny,
• trójkąt równoramienny,
• trójkąt różnoboczny.

Trójkąt równoboczny ma wszystkie boki i kąty takie same, a każdy z kątów wynosi 60°. W przypadku trójkąta równoramiennego dwa boki są równe, co powoduje, że kąty przy podstawie również są jednakowe. Z kolei trójkąt różnoboczny posiada boki i kąty o różnych długościach i wartościach.

Trójkąty mogą być także klasyfikowane według kątów:

• trójkąty ostrokątne mają wszystkie kąty mniejsze niż 90°,
• trójkąty prostokątne wyróżniają się jednym kątem prostym, wynoszącym 90°,
• trójkąty rozwartokątne mają jeden kąt większy niż 90°.

W każdym trójkącie suma miar kątów wewnętrznych zawsze wynosi 180°. Zrozumienie tych podziałów jest kluczowe przy rozwiązywaniu zadań geometrycznych i matematycznych w szkole.

Czworokąty – klasyfikacja i zastosowanie

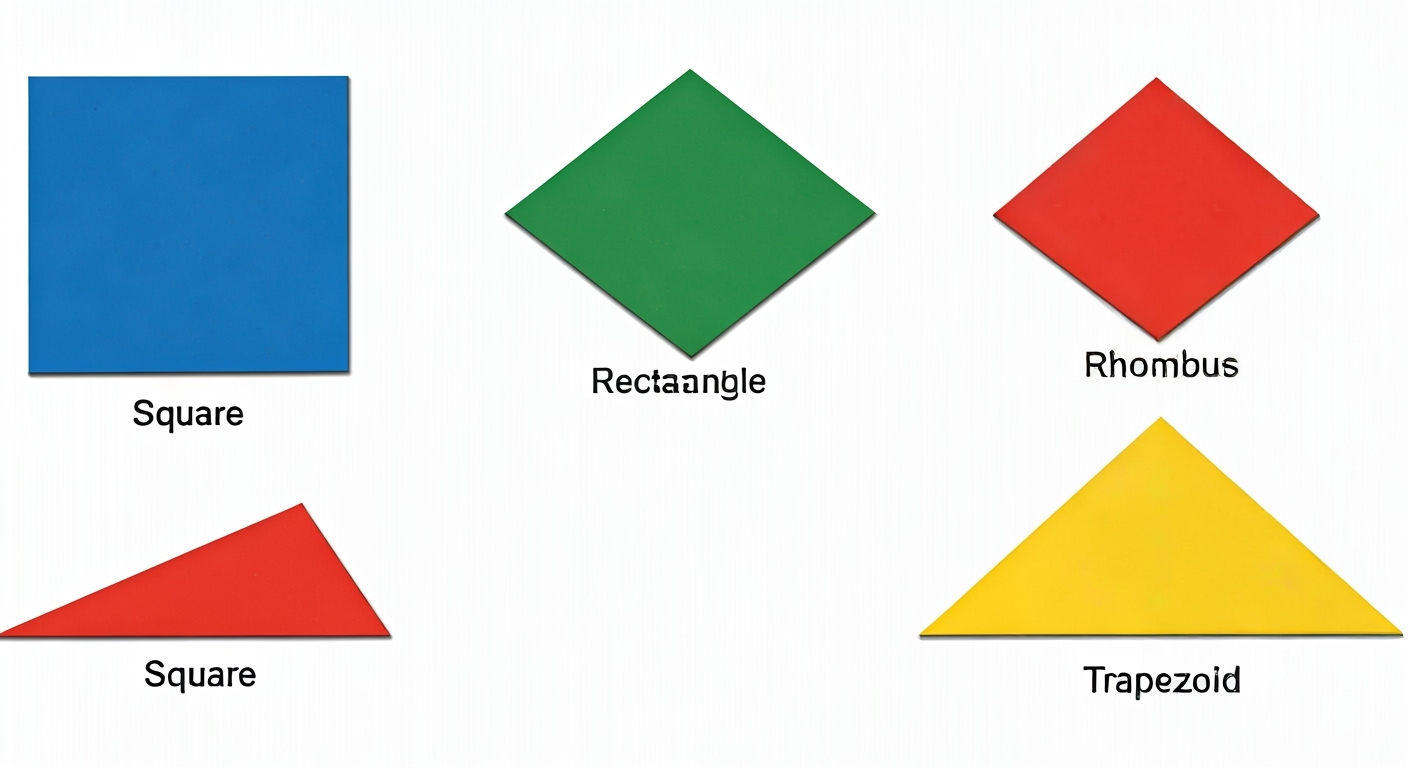
Czworokąty to figury geometryczne o czterech bokach i wierzchołkach. Istnieje wiele rodzajów takich figur, w tym:

• kwadraty,
• prostokąty,
• romby,
• trapezy.

Każdy z nich charakteryzuje się specyficznymi właściwościami wpływającymi na ich zastosowanie.

Na przykład:

• Kwadrat wyróżnia się równością boków oraz prostymi kątami, co czyni go niezastąpionym w projektach wymagających idealnej symetrii,
• prostokąty, dzięki dwóm parom równych boków, często znajdują zastosowanie w architekturze,
• romby, posiadające cztery równe boki, ale różnorodne kąty, są chętnie wykorzystywane w dekoracjach,
• trapezy, z jedną parą boków równoległych, są nieocenione w projektowaniu mostów i innych konstrukcji.

Zrozumienie właściwości czworokątów odgrywa kluczową rolę w edukacji matematycznej, a także w praktycznych dziedzinach inżynierii i projektowania.